已知g(x)在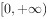
可导，且g(1)=1，若
，
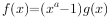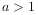，则导数
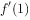的值是（ ）。
点x=0是函数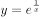
的（ ）。
设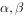
，是n阶向量，
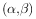是内积，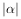
是向量的模长，则（ ）。
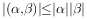
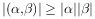
对于任意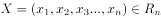
，若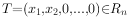
，则T是（ ）。
过点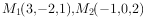
的直线方程是（ ）。
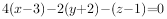
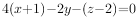
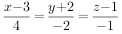
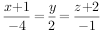
甲乙两人独立的对同一个目标进行射击，其命中率分别为0.4和0.5，则目标被命中的概率是（ ）。
普通高中数学课程标准突出的四条内容主线是（ ）。
下面不适合作为指数函数模型教学的是（ ）。
设h为常数，讨论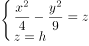
，在空间直角坐标系中所表示的空间类型。
已知向量组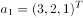
，
，
，
。
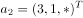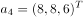（1）证明向量组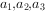
是三维空间的一组基；（4分）
（2）求向量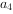
在基底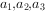下的坐标。（3分）
设二维随机变量（X,Y）服从***（n,m），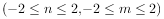
上的均匀分布，其中n，m都是整数。
（1）求随机变量X的概率分布；（3分）
（2）令Z=min{X,Y}，求随机变量Z的概率分布。（4分）
简述长方体模型在学习直线与直线、直线与平面、平面与平面的平行和垂直位置关系中的作用。（答出两条即可）
数学教学中要注意知识的**和**性，请写出高中数学中“函数单调性”密切相关的具体知识。（答出5条即可）
证明：函数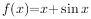
在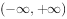
上一致连续。
写出对数的概念和3条运算性质，并结合对数的运算性质谈谈你对对数加法运算与乘法运算互相转化的认识。
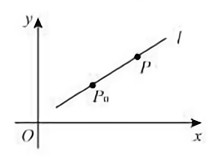
下面是某教师关于“建立直线的点斜式方程”的教学片段。
教师：如图直线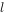
经过点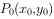
，且斜率为k，设P(x,y)是直线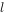上不同于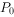
的任意一点，如何由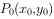，P(x,y)两点的坐标表示直线的方程？
学生甲：因为直线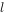经过点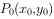，P(x,y)两点，由过两点的直线斜率公式，得 
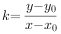，我认为这就是直线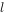的方程。
……
教师：直线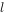上任意点的坐标(x,y)都满足关系式
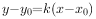吗？坐标满足关系式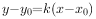的每一个点都在直线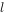上吗？
学生乙：由前面的直线方程就可以看出：直线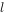上每一个点的坐标(x,y)都满足关系式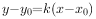；坐标满足关系式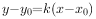的每一个点显然也都在直线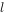上。
……
问题：
（1）学生甲的回答正确吗？为什么？
（2）学生乙的回答不严谨，请说明理由并完善。
高中数学课程要求“借助向量的运算，探索三角形边长与夹角的关系，掌握余弦定理”。
某教材部分内容如下：
1.余弦定理
我们知道，边长和它们的夹角分别相等的两个三角形全等，这说明，给定出边及其夹角的三角形是唯一的。也就是说，三角形的其他边、角都可以用这两边及夹角来表示。那么、表示的公式是什么？
探究
因为涉及的是三角形的两边长和它们的夹角，所以我们考虑用向量的点乘积来探究。
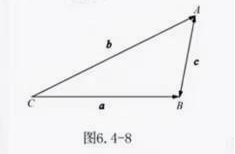
如图6.4.8，设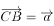
，
，
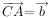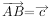，那么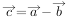
。
我们的正弦定理是用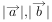
和C表示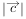
，联想到向量数量积的性质
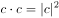，可以考虑用向量
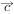加减运算（即）与其自身做点乘运算。
由①得
……
完成下列任务：
（1）根据上述材料，写出用向量方法证明余弦定理的过程；
（2）设计“余弦定理”这节课的教学目标，并确定教学重点；
（3）针对上述材料中“探究”的问题，设计3个课堂提问，引导学生从三角形的边角关系入手，逐步探索用向量方法证明余弦定理，并说明设计意图。
当前浏览器版本过低，建议升级到Internet Explorer
9及以上版本或者安装Chrome内核浏览器获得最佳浏览体验。