矩阵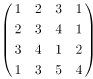 的秩是( )。
的秩是( )。
已知向量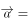
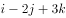 ,
,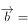
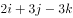 ,则
,则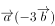 的值是( )。
的值是( )。
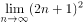
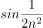 的值是( )。
的值是( )。
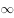
已知一条曲线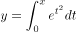 的一条切线与直线
的一条切线与直线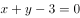 垂直,则该切线方程是( )。
垂直,则该切线方程是( )。
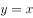
在空间直角坐标系中,将椭圆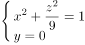 绕
绕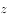 转一周,所得旋转曲面的方程是( )。
转一周,所得旋转曲面的方程是( )。
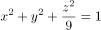
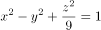
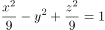
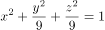
已知属于不同特征值的特征向量线性无关,若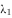 、
、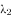 是矩阵
是矩阵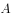 的两个不同的特征值。所对特征向量分别是
的两个不同的特征值。所对特征向量分别是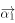 ,
,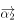 ,则向量
,则向量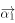 与
与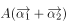 线性无关的充分必要条件是( )。
线性无关的充分必要条件是( )。
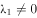
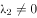
第十四届国际数学教育大会(ICME-14)于2021年7月在中国上海举行,ICME-14的会标如图1所示,其中没有涉及的数学元素是( )。

高中数学教学中的周期函数是( )。
已知向量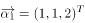 ,
,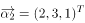 ,
,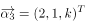 ,且行列式
,且行列式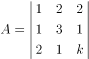
(1)若行列式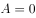 ,求
,求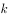 的值。
的值。
(2)当行列式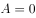 时,将向量
时,将向量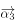 表示为
表示为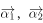 的线性组合。
的线性组合。
求由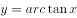 与直线
与直线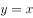 ,
,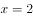 所围成平面区域的面积。
所围成平面区域的面积。
甲乙两人进行射击比赛,各射击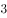 次,击中次数多者获胜。假设他们每次击中的概率均为
次,击中次数多者获胜。假设他们每次击中的概率均为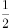 。且每次射击是相互独立的。
。且每次射击是相互独立的。
(1)求乙在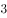 次射击中恰好击中
次射击中恰好击中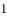 次的概率;
次的概率;
(2)已知甲在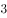 次射击中恰好击中
次射击中恰好击中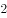 次,求甲获胜的概率。
次,求甲获胜的概率。
学生能够获得进一步学习以及未来发展所必须的“四基"和“四能”是普通高中数学课程的**之一,回答“四基”和“四能”分别是什么。
结合实例,简述什么是简单随机抽样和分层随机抽样。
已知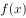 在
在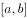 上连续,且
上连续,且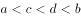 ,
,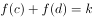 ,证明至少存在一点
,证明至少存在一点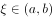 ,使得
,使得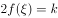 。
。
函数是中学数学的重要概念,回答下列问题:
(1)写出高中阶段函数的定义;(5分)
(2)阐述高中阶段函数的定义与初中阶段函数的定义的相同点与不同点。(10分)
在学习了同角三角函数的公式后,老师给学生布置了道题目。
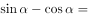
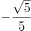 ,
,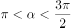
求 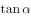 的值。
的值。
一名学生的求解过程如下:
解:依题意和同角三角函数基本**得: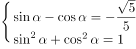 ;
;
消去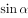 ,得
,得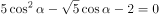 ;
;
进而得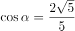 或
或 ;
;
因为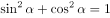 ;
;
所以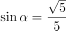 或
或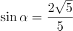 ;
;
所以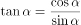
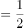 或
或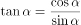
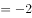 ;
;
因为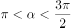 ;
;
所以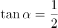 。
。
问题:
(1)单一主观题指出这名学生在求解过程的错误;(6分)
(2)给出上述题目的正确解法。(6分)
(3)根据此题的错误之处,分析这名学生在运算和逻辑推理方面的不足。(8分)
下面是某高中数学教材“点到直线的距离公式”一节的内容片段:
探究如图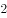 ,已知点
,已知点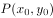 ,直线
,直线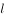 :
: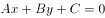 ,求点
,求点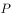 到直线
到直线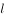 的距离?
的距离?
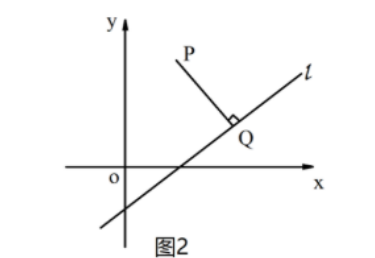
点P到直线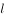 的距离,就是从点
的距离,就是从点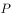 到直线
到直线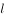 的垂线段
的垂线段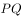 的长度,其中
的长度,其中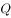 是垂足(图
是垂足(图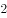 )。因此,求出垂足
)。因此,求出垂足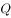 的坐标,利用点到直线的距离公式求出
的坐标,利用点到直线的距离公式求出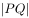 ,就可以得到点
,就可以得到点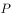 到直线
到直线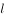 的距离。
的距离。
设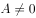 ,
,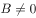 ,由
,由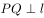 ,以及直线
,以及直线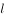 的斜率为
的斜率为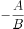 ,可得
,可得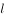 的垂线
的垂线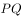 的斜率为
的斜率为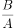 ,因此,直线
,因此,直线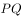 的方程为
的方程为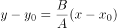 ,即
,即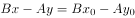 。
。
解方程组
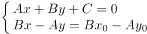
得直线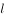 与
与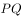 的交点坐标,即垂足
的交点坐标,即垂足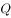 的坐标为:
的坐标为:
……
根据上述内容,完成下列任务:
(1)补充“点到直线的距离公式”的推导过程;(10分)
(2)设计这部分内容的教学目标;(8分)
(3)根据教学目标设计这部分内容的教学过程(含课堂导入、公式推导、巩固提高、课堂小结及设计意图)。(12分)
