下列选项中,运算结果一定是无理数的是( )。
在空间直角坐标系中,由参数方程 ,(0 ≤ t < 2π)所确定的曲线的一般方程是( )。
,(0 ≤ t < 2π)所确定的曲线的一般方程是( )。
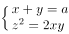
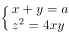
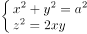
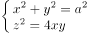
已知空间直角坐标与球坐标的变换公式为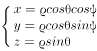 ,(ρ ≥ 0,-π < ϕ ≤ π,
,(ρ ≥ 0,-π < ϕ ≤ π,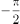 ≤θ ≤
≤θ ≤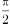 ),则在球坐标系中, θ=
),则在球坐标系中, θ=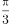 表示的图形是( )。
表示的图形是( )。
设 A为 n 阶方阵,B是 A 经过若干次初等行变换得到的矩阵,则下列结论正确的是( )。
已知 f(x)= 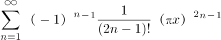 ,则 f(1)=( )。
,则 f(1)=( )。
若矩阵 A=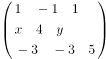 有三个线性无关的特征向量,λ=2 是 A的二重特征根,则( )。
有三个线性无关的特征向量,λ=2 是 A的二重特征根,则( )。
下列描述为演绎推理的是( )。
《义务教育数学课程标准(2011 年版)》从四个方面阐述了课程目标,这四个目标是( )。
一次实践活动中,某班甲、乙两个小组各 20 名同学在综合实践基地脱玉米粒,一天内每人完成脱粒数量(千克)的数据如下:
甲组:57,59,63,63,64,71,71,71,72,75,75,78,79,82,83,83,85,86,86,89;
乙组:50,53,57,62,62,63,65,65,67,68,69,73,76,77,78,85,85,88,94,96。
问题:
(1)分别计算甲、乙两组同学脱粒数量(千克)的中位数;(2 分)
(2)比照甲、乙两组数据,请你给出 2 种信息,并说明实际意义。(5 分)
试判断过点 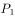 (2,0,1),
(2,0,1),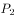 (4,3,2),
(4,3,2),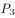 (–2,1,1) 的 平 面 π 与 平 面
(–2,1,1) 的 平 面 π 与 平 面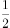 x+2y–7z+3=0 的位置关系,并写出一个与平面 π 垂直的平面方程。
x+2y–7z+3=0 的位置关系,并写出一个与平面 π 垂直的平面方程。
已知方程 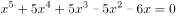 的两个实数解为1与–2,试求该方程的全部实数解。
的两个实数解为1与–2,试求该方程的全部实数解。
用统计方法解决实际问题的过程,主要包括哪些步骤?
评价学生的数学学习应采用多样化的方式,请列举四种不同类型的评价方式。
设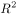 为二维欧氏平面,F是
为二维欧氏平面,F是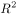 到
到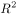 的映射,如果存在一个实数ρ,0 < ρ < 1,使得对于任意的 P,Q ∈
的映射,如果存在一个实数ρ,0 < ρ < 1,使得对于任意的 P,Q ∈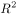 ,有 d(F(P),F(Q))≤ ρ d(P,Q)(其中 d(P,Q)表示 P,Q 两点间的距离),则称F是压缩映射。
,有 d(F(P),F(Q))≤ ρ d(P,Q)(其中 d(P,Q)表示 P,Q 两点间的距离),则称F是压缩映射。
设映射 T: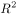 →
→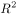 ,T((x,y))=(
,T((x,y))=(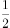 x,
x,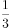 y), ∀ (x,y) ∈
y), ∀ (x,y) ∈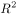 。
。
(1)证明:映射 T 是压缩映射;(4 分)
(2)设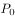 (
(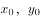 )为
)为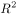 中任意一点,令
中任意一点,令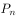 =T(
=T(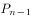 ),n=1,2,3,…,求
),n=1,2,3,…,求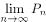 。(6 分)
。(6 分)
函数是中学数学课程的主线,请结合实例谈谈如何用函数的观点来认识中学数学课程中的方程、不等式、数列等内容。
案例:
甲、乙两位数学教师均选用如下素材组织了探究活动,如图 1 所示,这是一个三级台阶,它的每一级的长、宽、高分别为50cm,25cm和15 cm,A和B是这个台阶的两个相对端点,B点上有一只蚂蚁,想到A点去吃食物。请你想一想,这只蚂蚁从B点出发,沿着台阶面爬到A点的最短路线是什么?
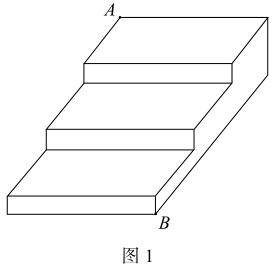
两位教师的教学过程如下:
【甲教师】
用大屏幕展示问题情境,组织小组讨论,学生开始读题,教师巡视过程中看到有的同学把台阶画出来,与教学预设不符,立即中止了大家讨论,指着题目说:“同学们请注意读题,是‘沿着台阶面’,你们把这张图画出来有什么用?”
在接下来的讨论中,教师又遇到新情况,有的学生画展开图,却把尺寸弄错了,于是教师终止思考。
【乙教师】
展示情境,将问题进行分析,出示了一张台阶模样的纸片,边说边将纸片拉直,如图 2 所示,然后让大家研究。很快,有同学说出答案,教师解释了一下,同学们都明白了。
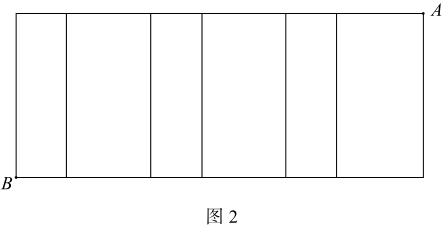
甲、乙教师课后交流:两个教师在教学中均有探究。
(1)《义务教育数学课程标准(2011 年版)》指出,“有效的数学教学活动是教师教与学生学的统一”,教师应成为学生学习活动的组织者、引导者、合作者。请说明两位教师的教学是否符合要求;(6 分)
(2)两位教师组织的探究活动各自存在什么问题,请简要说明并简述理由;(6 分)
(3)组织数学探究活动,需要注意哪些事项?请说明。(8 分)
《义务教育数学课程标准(2011 年版)》附录中给出了两个例子:
例1. 计算 15×15,25×25,…,95×95,并探索规律。
例2. 证明例 1 所发现的规律。
很明显例1 计算所得到的乘积是一个三位数或者四位数,其中后两位数为25,而百位和千位上的数字存在这样的规律:1×2=2,2×3=6,3×4=12,…,这是“发现问题”的过程,在“发现问题”的基础上,需要尝试用语言符号表达规律,实现“提出问题”,进一步实现“分析问题”和“解决问题”。
请根据上述内容,完成下列任务:
(1)分别设计例 1、例 2 的教学目标;(8 分)
(2)设计“提出问题”的主要教学过程;(8 分)
(3)设计“分析问题”和“解决问题”的主要教学过程;(7 分)
(4)设计“推广例 1 所探究的规律”的主要教学过程。(7 分)
